Recorduri românești la Scrabble
CÂTE UNA DIN FIECARE
La 1 aprilie 1984 tânărul și talentatul atlet polisportiv Tinel ALDEA din Târgovişte propunea cititorilor Revistei Rebus problema cu titlul de mai sus.
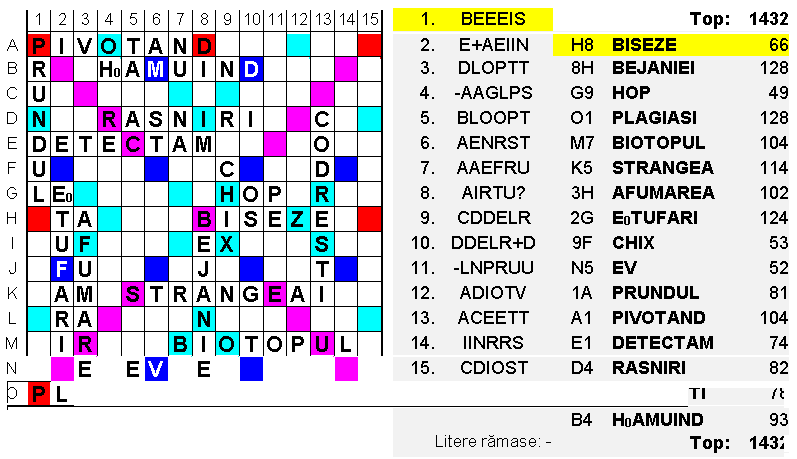
Să se realizeze o grilă cu punctaj maxim, folosind câte o literă din fiecare, inclusiv un joker, care poate înlocui orice literă, după regulile de la Scrabble integral. Valoarea literelor nefolosite (din cele 23) se scade din punctajul total (DEX, DLRM, DOOM, f.f.f.).
Clasamentul din 1984 (140 concurenţi):
1. Serghei PETROVICI 796
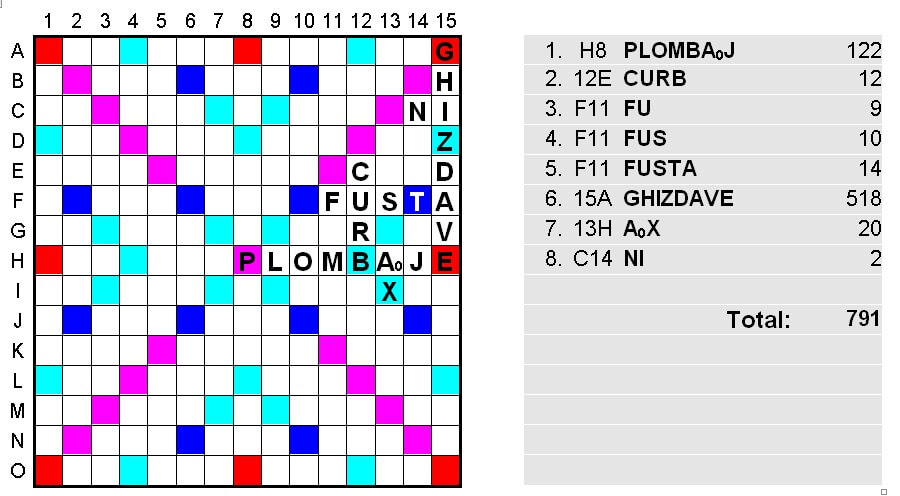
2. Leontin Dimitru MOŢ 791
2. Tinel ALDEA 791
2. Florin MUREŞAN
791
2. Ion BRÎNDUŞOIU 791
2. Nicolae OPRIŞIU 791
2. Tudor CANŢER
791
2. Ovidiu OPRIŞIU 791
2. Daniel CONSTANTINOIU 791
2. Petre PAIU 791
2. Marius CORNELIU 791
2. Marilena Panait 791
2. Marian DUŢU 791
2. Simion SABO 791
2. Cezar GROZESCU 791
2. Grigore Radu SCURTU
791
2. Augustin MARICA 791
2. Ilie SOCOLOV
791
2. Maestra Sportului Claudia MIHAI
791
2. Dan TASE
791
Soluţia record, realizată de Serghei PETROVICI din București:
O variantă cu 791 p:
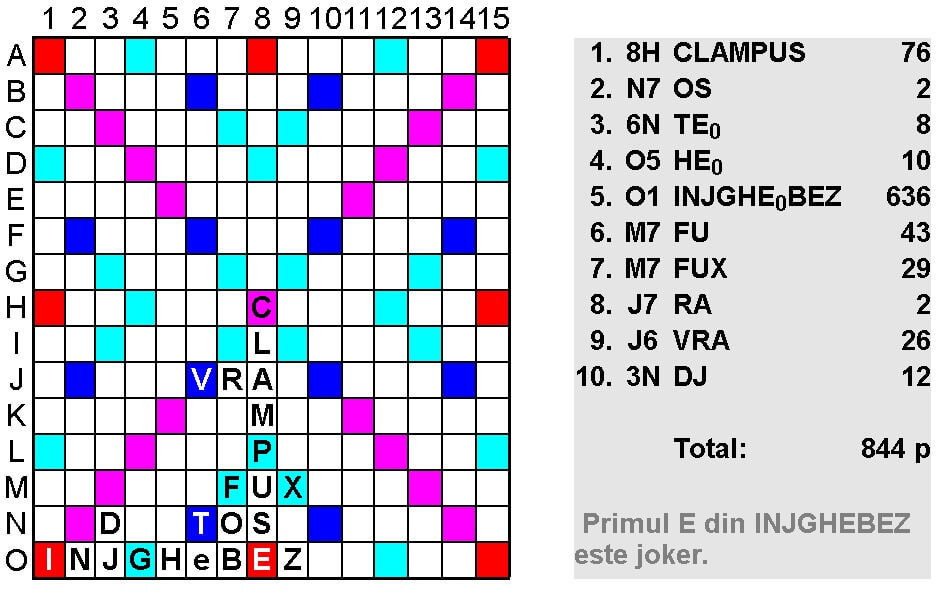
Recordul actual este de 844 p și aparține din 10 iulie 2011 Maestrului Sportului Gheorghe Roman, Câmpulung Moldovenesc:
